3.定まった量と変わる量
・(まとめ)要は、定数と変数の概念の紹介。例として、遠心力に影響される重さと、温度に影響される棒の長さ。
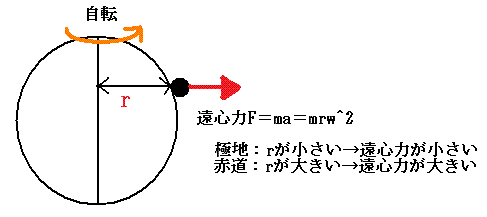
↑赤道だと遠心力が一番大きく働くので、その分だけ重さは軽くなるという話。等速円運動と慣性力の知識が前提とされているw
1.量の測定
・(まとめ)『量』を測定すると、その量は『数』と対応させることができる。そして『数』は『単位』の取り方によって変わるーーーーということが言いたいらしい。そりゃそうだ。
2.数
・(まとめ)数には整数、有理数、無理数があり、四則演算が定義される。数には大小があるという話になり、絶対値と三角不等式の紹介。
・『共測』とか『非共測』とかいう見慣れない言葉がいきなり出てきて戸惑う。『共測』だと有理数だし、『非共測』だと無理数らしい。…何だこれは。定義を教えてくれ。ちなみに『きょうそく』で変換できないぞ、チクショーめ。
単位量との関係で『共測』やら『非共測』やらと区別するらしいが、それでは単位量を無理数に決めた場合、無理数の整数倍は『共測』と言うことはできやしないか?
・循環小数は有理数、循環しない無限小数は無理数。はーい、了解。循環小数をa/(1-r)を使って分数で表すことには触れていない。
・p.3「十進法を用いると、無理数はたがいに大きさを比べることができ、」→確かにそうだが、それは十進法じゃなくても何進法でも良いわけだから、わざわざ書く必要は無くね?
・「任意の有限小数は循環する数字9をもつ無限小数に書きかえることができる」「全ての無限小数にはそれぞれ一定の実数が対応する」とあっさり説明。
3.定まった量と変わる量
・(まとめ)要は、定数と変数の概念の紹介。例として、遠心力に影響される重さと、温度に影響される棒の長さ。

↑赤道だと遠心力が一番大きく働くので、その分だけ重さは軽くなるという話。等速円運動と慣性力の知識が前提とされているw
4.区間
・(まとめ)閉区間と開区間の概念の導入。普通、今の日本では閉区間を[a,b]で表すと思うが、この本では全て開区間の(a,b)で表している。これはチト紛らわしい。
・定義域、値域という言葉を使わずに『変域』という言葉を使っている。
5.函数の概念
・(まとめ)函数の概念の定義。
・「函」数って漢字の使い方を見ると、「古っ!」と思ってしまうw
・p.6、高校のときに『ボイル・シャルルの法則』と習ったヤツが、この本では『ボイル・マリオットの法則』と書いてある。昔はこう呼んだのだろう。同じように理想気体の状態方程式が『ボイル・マリオット・ゲイ・リュサックの法則』と書かれている。長いし、ゲイ=リュサックが分かれちまってるぞw
6.函数関係の解析的表現
・(まとめ)函数が方程式によって表現されている場合、『解析的に表現された』と言う。「『函数』の一般概念と、『解析的表現』という概念とを混同してはならない」。そして陽函数の例を呈示している。
7.陰関数
・(まとめ)前節で陽函数を扱ったので、今度は陰函数の紹介。
8.表による方法
・(まとめ)「函数表のもつ重要な意味は、函数の解析的表現が知られていない場合でも、表によって函数が表されるという点である」。表→おもに函数表のこと。例として九九。そういや、『比例部分の原理』なんてスッパリ忘れていましたわ。
9.数をグラフによって表す方法
・(まとめ)数直線による数の表現についての節。ここで言っている『線分』というのは、『(1次元の)有効線分』のことで良いのだろうか。
10.座標
・(まとめ)9節の内容を今度は2次元に。座標による数の表現についての節。特記事項なしw
11.曲線とその方程式
・(まとめ)曲線のグラフとはどういうものか、という節。グラフ上の全ての点は方程式を満たし、また方程式を満たす点は全てグラフ上にあるということ。ここも特記事項なしw
12.一次函数
・(まとめ)y=ax+b の式とそのグラフについて。高校の頃、ウンザリするほどやった式ですな。
13.増分、一次函数の基本性質
・(まとめ)一次函数の続き。
・「増分は正の値にも負の値にもなることができるから、"増分"だけ付け加えられた量が必ずしも増加しないことに注意しよう」。
14.一様な運動のグラフ
・(まとめ)点が一つの道を運動するとする。時間tと正負の値をとる道のりsについて、s=f(t)を考える。『一様な運動である』とは、等速運動の場合と定義する。
・いわゆる受験物理では『道のり』とは総移動距離(≧0)のことを指すので、この本で言う道のりは、一次元の変位と言った方がいいか。同様にp.20「負の速さ」は、負の速度か。
15.実験式
・(まとめ)実験データを直線で近似することがあるよ、と言っているだけ。詳しい話はなし。
・p.20「実験式を表す直線は"糸を張る"方法によってえがくのが最も簡単である」。←糸を張る方法ってのが何だか分からないぞ。
16.二次の放物線
・(まとめ)放物線の性質とグラフについて。
・これも高校でイヤというほどやった。『二次の放物線』というタイトルだが、放物線ならば必ず二次なので『放物線』だけで良くね?と思ったが、次節は三次の放物線。この本の『放物線』の定義を知りたい。
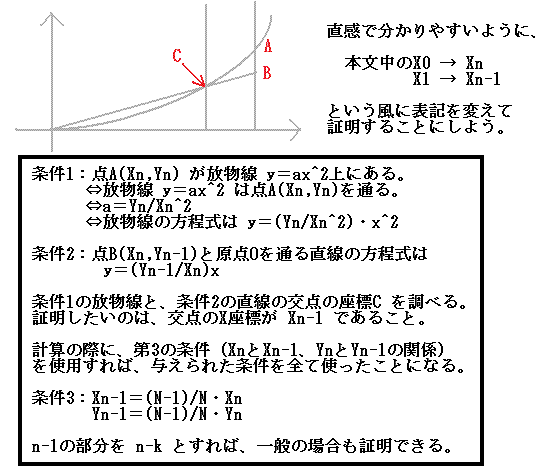
・p.22下段〜p.23上段の証明がスッキリしなかったので、自分流に証明してみた。証明の流れは以下の通り。この流れで確かめることができた(完全な証明は、数式をhtmlファイルで示すのがチト大変なので省略…)。
17.三次の放物線
・(まとめ)三次函数の性質とグラフについて。特記事項なし。
18.反比例の性質
・(まとめ)双曲線の性質とグラフについて。
・p.24中段の証明がスッキリしなかったので、自分流に証明してみた。証明の流れは以下の通り。こちらは三角形の相似を使わず、3点O,P,Qが同一直線上であることを利用している。ま、同じことではあるのだが。

19.ベキ函数
・(まとめ)べき函数の性質とグラフについて。
・『ベキ』が片仮名だw
・今更気づいたが、この本はある函数が曲線上の点を何点を与えると一意に決まるか、逐一説明しているな。
・図22、図23で各直線が交わっている点が(0,0)ではなく(1,1)であるところに注意。
・p.27〜p.28の証明がスッキリしなかったので、自分流に証明してみた。証明の流れは以下の通り。ここでは自分の直感に沿うように少しだけ証明法を変える。Y軸側で結ぶ線分を T1-R2, T2-R3 という風に変える。

20.逆函数
・(まとめ)逆函数の定義と性質の説明。
・逆函数を得る操作を『反転』と呼ぶ。
21.函数の多価性
・(まとめ)一価と多価、増加函数と減少函数の説明。
・そういえば、『初等函数』という言葉を何の説明もなく使ってないか?この本。
22.指数函数と対数函数
・(まとめ)指数函数と対数函数の定義とグラフの紹介。指数函数の諸々の定理については44節で後述される。この本では対数函数の定義は素直な高校流で、指数函数の逆函数としての定義が採用されている、
・p.32の指数部分の印刷が薄くて読めねーよw。類推で分かることは分かるのだが…。
・対数の具体例として、『対数尺』と『対数方眼紙』が紹介されている。対数方眼紙の方は実験で何度も使ってるので問題ないが、対数尺のほうは実物を見たことないし具体例も紹介されてないので、この本だけじゃよく分からん。
23.三角函数
・四つの基本的な三角関数として、cot(=1/tanθ)がsin, cos, tan とほぼ同列に扱われているのが目新しい感じ。てか、secとcosec 涙目www なぜコタンジェントだけを優遇?
・p.35の下から6行目の漢字「帶」が旧字体で読めない。ググったら、類推通り『帯』の旧字体だった。
・p.36の図37をさらに説明する公式として、tan (π/2 - θ) = cot θの証明をする。
証明にあたり、tanの加法定理を使いたくなるが、tan(π/2)が使えないので手が止まる。
さあ、どうすれば良いか。
ここではtanθ=sinθ/cosθとして、その後にc,s各々の加法定理を使うことにする。
(左辺の分子)=sin(π/2-θ)=s(π/2)cθ−sθc(π/2)=cθ
(左辺の分母)=cos(π/2-θ)=c(π/2)cθ+s(π/2)sθ=sθ(θ≠nπ)
ゆえに(左辺)=cθ/sθ=cot θ
これで証明された。
・p.37『単純調和曲線』、『複合調和曲線』なる言葉の紹介。フーリエ変換をイメージしてますな。
24.逆三角函数
・式(23)の公式が「容易に分かる」で済まされているので、ここで証明をしておく。これって本当に「容易に分かる」かねえ?グラフを見たらそれっぽいけど、証明は結構難しいと思うぞ。
証明の方針:我々は既に三角函数の多くの公式について既知であるため、この場合も逆三角関数から三角関数に戻って計算する。証明は…サイエンス社の微積演習書p.15に一応2式とも、そのまま載ってる。ポイントはともに z =π/2-y (⇔ y+z=π/2) を使うところ。定義域や値域を考えると混乱しやすく、それなりに技巧的な証明だと思う。ここでは自分流の証明も載せておこう。

※サイエンス社の解答にあるように y=sin(π/2 −x), z=cos x として示すのは私にはこなれすぎてるし、さらに同じxを使って良いという保証について今一つスッキリしないので上のような証明にしてみた。一応、『一価であり逆函数をとれるかどうか』ハッキリさせるようにしている。
・arctanとarccotの証明では、[23]項で個人的に証明した、tan(π/2-θ)=cotθ を利用する。この公式を利用して、arcsinとarccosの公式とほぼ同じ形で証明することができる。

・12項から24項までは初等函数の定義とグラフを概説していたが、何点とれば函数が一意的に決まるのかと、作図法について逐一説明していた。
・今のところは、とりたてて分かりやすい本だとも思えない。スミルノフ的にも第1章は復習として概説しただけーーーであることを祈ろう。
・『有界』は出てきてるけど『上限』は出てきてない。
・この項からやっと面白くなってきた!
・p.43「limはラテン語limes(極限)の初めの部分をとったものである。」ほお、知らなかった。
・p.42最終行について。「Nは商を超えない最大の整数をとればよいことがわかる」とあるが、別にNは最小である必要はないのでは?(log10ε/log10q)よりも大きいどんな数でも良いのでは?
・p.46の最終行のkに関する話、kがイキナリ登場してるので何なのか分からず、何の話かサッパリ分からない。
・p.47のNについても、前項でツッコミ入れたように別にNは最小である必要はないのでは?
・p.49、有限一定値+無限小を作って、これを四則演算するのが面白い(無限小の四則演算)。ε-δまでは使ってないが、これでも十分証明されている気がする。というか、高校数学の教師でそこそこ厳密な人はこの証明をしてたな。
・p.50「これらの定理は、−−−がそれぞれ極限値に収束するとき、和・積・商の極限値の存在を保証する。」
・収束の説明で一貫して「原点が中点となるような線分」という表現が使われているが、この説明は本書以外ではあまり見たことないな。絶対値を使って考えるのだから、この表現使うのは良いと思うんだけど。思うに、絶対値と不等式というのがε-Nの1つのキーワードですな。
・p.52、この本ではx→∞とx→+∞を区別している。
・
26.無限小
・(まとめ)『有界 (p.45で定義が修正される) 』、『収束』、そして『ε-N論法(ただしこの言葉は出てこない)』で数列の収束が語られる。まずは0に収束する数列の話:{r^n}(0
27.変数の極限値
・前項では0に収束するものだけを扱ったが、この項では一般の数 aに収束するものを扱う。
28.基本定理
・(まとめ)前項では0に収束するものだけを扱ったが、この項では一般の数 aに収束するものを扱う。
29.無限大
・(まとめ)
2.
・(まとめ)
<第2節のまとめ>
・極限の話になって面白くなってきた。